The Immortal Unvaccinated Problem

and Follow-up to the ONS row

Summary (click to expand):

Why Immortal Unvaccinated People Happen

I have covered this problem before, but it deserves an emphatic review.

Studies, broadly speaking, are not omniscient. Vaccine studies especially so. Rather than even representing a “hunt” for some truth, most vaccine studies in practice operate like trapping: Some arrangement of boxes is set up, and the authors come back out the next morning and see what numbers fell into the boxes. The authors do actually not know how many animals are in the forest; they only know how many are in their boxes. The study is not omniscient.

Why this flaw does not benefit vaccines

The reader may imagine that such limitations would intrinsically, deliberately promote illusions of vaccine efficacy, simply by the principle of the trappers hating the unvaccinated. Indeed, “trapping”-based study designs have been deliberately developed to promote illusions of vaccine efficacy, but these designs were previously proven on different diseases, and have no intrinsic valence as far as SARS-CoV-2.

Here I speak explicitly of test-negative case control studies, which use a design that has no logical value. In other words, no one can possibly know what the result of any test-negative study means. It was simply found in practice that such studies derived the appearance of flu vaccine efficacy, and so the irrational design became something of an industry standard. This does not mean we should assume test negative case control studies can reveal negative truths about vaccines any more accurately than they can positive truths. (And yet many Covid vaccine critics are profligate TNCC-quoters, doing no one any service.)

In general, however, the “trapping” design disfavors measured interventions, in this case a set of experimental vaccines for SARS-CoV-2. Reporting rates of infections requires knowing how many animals are in the forest. But the trappers don’t know how many animals are in the forest.

The typical example here are government-operated or associated reports or studies. These start with a list of animals that the government thinks are in the forest, and then subtracts the animals it knows have the intervention (akin to trappers first going around and attaching anti-trap devices to animals, and noting the number of animals who they attach devices to, and subtracting this from the previous estimate of total animals).

The reader can presumably see how this problem could potentially cut both ways (discussed in footnote¹). Suffice to say this is in practice effectively a one-sided problem.

As another metaphor, imagine a classroom, with a corresponding attendance roll. The vaccinated — i.e. those the report-makers or study-authors know to be vaccinated — are akin to kids who have called out “here” at the beginning of class. The “unvaccinated” are simply all kids who have not called out “here.” So how does the report or study actually know they are even in the room? (It doesn’t.)

Whatever the other measured outcome is — officially recorded infections, especially — how could it possibly be equally likely that the kids who did not say “here” would appear in the system as those who said “here”? Some of them aren’t even “in the room.” If you were recording “wrong answers on tests;” the result that kids who actually came to class that day got more wrong answers wouldn’t be surprising. Granted, some who didn’t say “here” might have come to class; and some who say “here” might leave early; but mostly you have just created a population of immortal unvaccinated people. Many of them have already dropped out of the system, and can’t be recorded as infected.

Worse in high-uptake systems (sometimes)

This problem exerts the strongest distortions in regions with extreme vaccine uptake. I.e., if your health system’s list of estimated population includes 1% of people who are no longer able to interact with the system, then as long as 10% of people really do forgo the vaccine, the immortality discount is marginal. If another 6% get the vaccine, then the discount is substantial.

However, this problem can either be counteracted or exacerbated by differences in testing rates; such that high-uptake health bureaucracies like New York State and more heterogenous regions might report similar results.

In general, however, infection rates results reported in high-uptake regions and age groups should be regarded with extreme skepticism. This includes the UKHSA reports, which calculated the “unvaccinated” population by subtracting people with system-inclusive vaccine records from the government’s list of people invited for a vaccine. Everyone who was no longer really “in the classroom” again defaulted to “unvaccinated,” and could not be recorded as infected. This is the most likely reason why the UKHSA published results that were so discordant with more heterogeneous systems (e.g. the Israel dashboard), but concordant with a few other high-uptake systems (e.g. the Iceland dashboard).

Why the ONS data is better, but also biased

Now we consider this problem in light of the ONS data, recently discussed here:

ONS Ball

Whereas the UKHSA simply used the list of individuals invited for vaccination, the ONS tables are based on the Public Health Data Asset:

The PHDA is a linked dataset combining the 2011 Census, the General Practice Extraction Service (GPES) data for pandemic planning and research, and the Hospital Episode Statistics (HES)

This adds a different way and requirement of saying “here” — being in the census — so that there should be less difference in ability to interact with the system on the measured outcome (in this case, death, either with Covid-19 listed as the primary cause (“Covid-19 death”) or not) vs. the UKHSA. (By definition, the NIMS list includes people not recorded on the recent census, or there would be no exclusions in the ONS set.)

This potentially excludes some “in the room” unvaccinated, yes — those who came to class but did not say “here.” Whatever portion of the excluded unvaccinated are in class is irrelevant, however, to whether you have ensured that the included unvaccinated are in the class. Your unvaccinated denominator is now accurate for your recorded events.

source: ons.gov.uk (accessed February 23, 2023.) This is linked in the “Notes” section of the ONS spreadsheet.

While the notes fall short of explicitly defining which ONS tables use the PHDA and which don’t, my interpretation of this set-up (that the by-age monthly tables use PHDA) has since been affirmed by Sarah Caul in numerous tweet-threads. A more detailed explanation has also been supplied by one Michael George:

source: @Mike_aka_Loiqx (twitter.com)

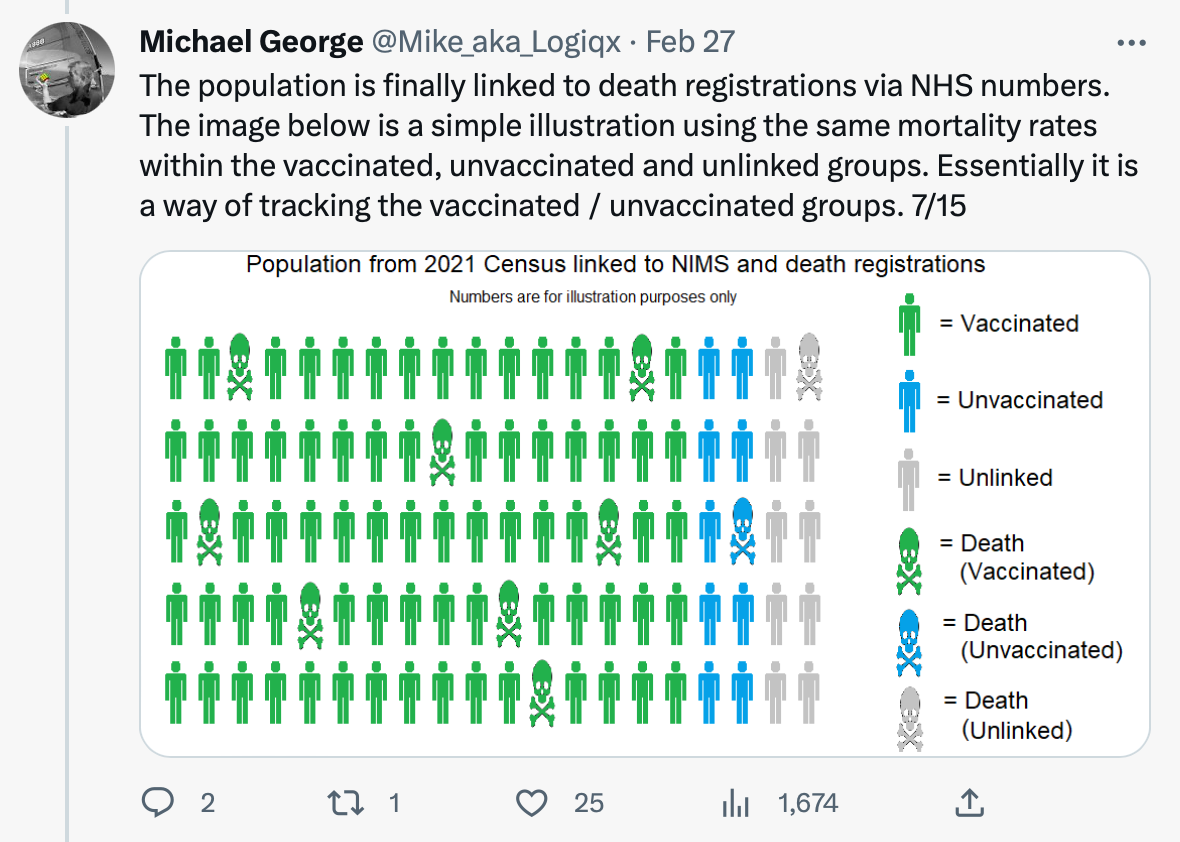
But does this exclusion introduce biases?

Yes, it probably does. The question of whether to consider these probable biases a “flaw” is difficult.

I have previously argued that the ONS-included “unvaccinated” might have a bias for unhealthiness based on requiring General Practice Extraction Service inclusion; however, this doesn’t seem to be an actual requirement (the only requirements are the census overlaying with NIMS). There might not be such a bias here after all.

Instead, and as I have argued for a year,² the biggest bias seems to be against giving Covid vaccines to those who are about to die. This results in the unvaccinated “performing” like the last kids selected for a basketball team — the unvaccinated contain all the people who weren’t expected to “help the team.”

However, this isn’t a bias with the ONS data, but with vaccination in the UK in general.

It reflects something that really occurred in vaccine-choices in the UK; and that, regardless of whatever one would expect, severely depresses the apparent death-rate of the recently-vaccinated below baseline. Support for the generic nature of this bias in the UK is found in other literature:³

Stirrup, O. et al.

Elderly UK nursing home residents who are receiving end of life care are:

1. Likely to die soon.

2. A large driver of human deaths at any given moment.

3. Unlikely to receive Covid vaccines.

The problem with declaring this bias a “flaw” in the ONS data is that leads to the wrong solution.

If the ONS data is showing what happens when “our side” gets what it has asked for (“show us the data!”), then it means our side needs to ask different questions.

Instead of throwing phones across the room and calling the ONS data a slut, in other words, the ONS data should be embraced for illuminating paradoxes that make determining and revealing deaths caused by vaccination difficult. The sooner that is done, the sooner work can start toward figuring out how better to measure the effects of the vaccines.

Sadly, it likely requires complex models that will be difficult to understand and subject to high amounts of controversy. For example, I used such a model to show how the vaccines could be increasing myocarditis rates in older recipients despite their having lower overall rates. It wound up looking like this:

From “Technical Difficulties.”

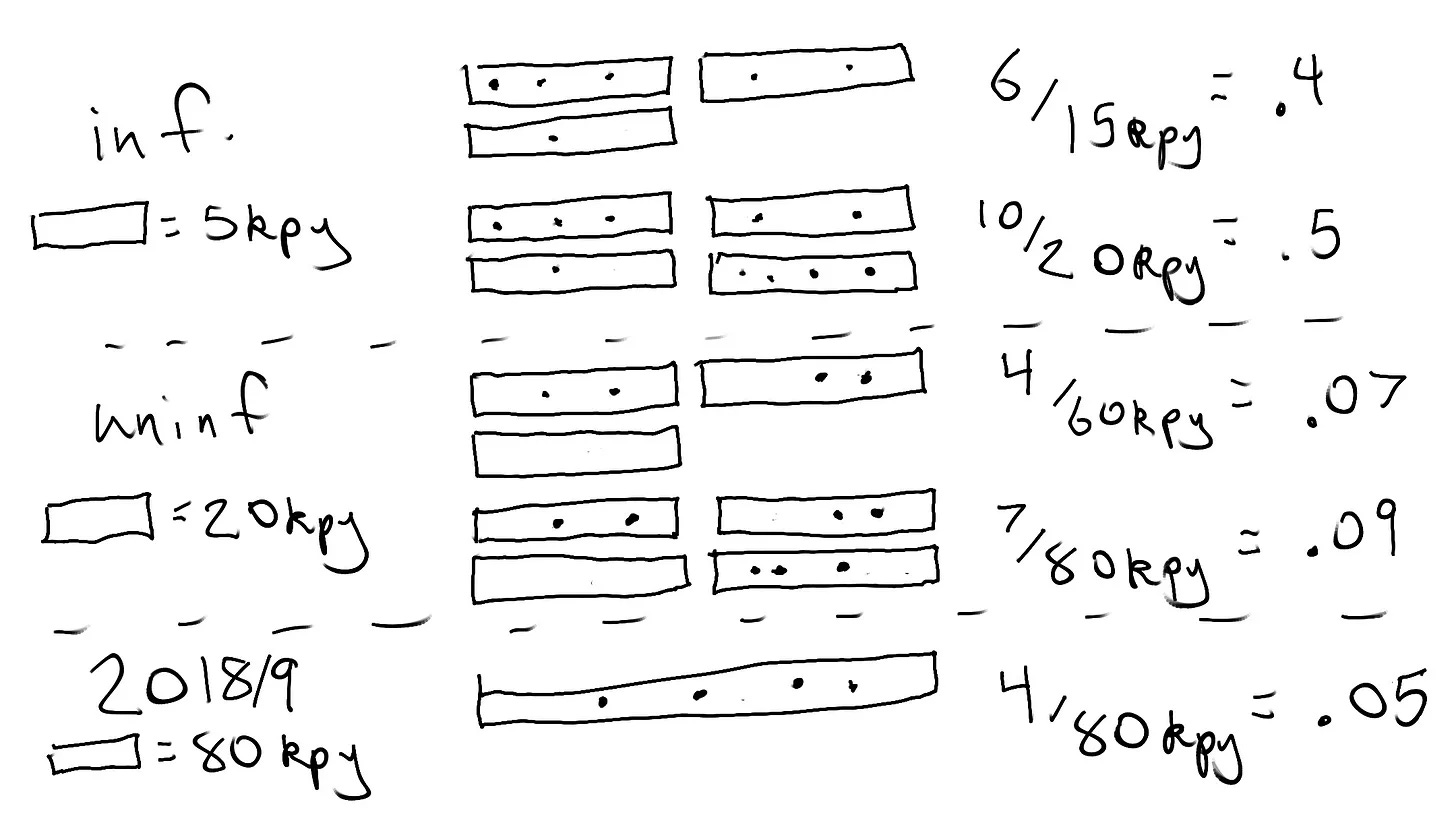
It won’t be fun. Like in the South Park episode, the temptation will be strong to just go back to the giant gay humping pile.

As with my previous post, I would like to again encourage readers to understand that this is all that is really substantiated or substantiate-able in all the complaints about the ONS data. It is not “flawed;” it is surprising and hard-to-understand in a way that challenges expectations. (Note that paragraph this is essentially my response to Niel and Fenton’s critique, “Postmodern science delivers immortality benefits,” which I find to offer little beyond an assertion that the ONS data should be dismissed because the death rates are surprising and hard-to-understand. My response to Clare Craig’s “ghosts” analysis is in Footnote 1, below.)

If you derived value from this post, please drop a few coins in your fact-barista’s tip jar.

click button or visit https://ko-fi.com/unglossed

The unrecorded vaccinated question

1. The question is whether some vaccinated are not recorded as such (i.e., they got injected outside of the system, which is more a problem in the US than the UK), and how this would affect results.

In general, this cannot create any benefit for the vaccines relative to the unvaccinated. If you are comparing the qualities of ice and water, it doesn’t matter if some of your ice actually has water — it will still be different than water in “ice-ness.” Only if both sides were totally blended would the difference disappear; and so the negative or positive effect of vaccines measured relative to not-vaccines can be diluted but not reversed.

The difference might seem to be that unrecorded vaccination-havers are also, like everyone else not recorded as vaccinated, less likely to interact with the recording system on negative measures. However, this can not benefit the vaccine, since unrecorded vaccination-havers are deemed “unvaccinated” — i.e., they should add bias against the vaccine.

And Clare Craig’s “ghosts”

The final exception here is if being an unrecorded vaccine-haver is somehow associated with the negative outcome; i.e., if dying or being infected after injection leads to lower likelihood of being recorded as injected.

Outside of overt fraud, this would not apply to the ONS data — deaths after vaccination are recorded as vaccinated deaths; there is a specific category for the just-injected; they aren’t “miscategorized” as unvaccinated. Sarah Caul has affirmed this on twitter multiple times.

There is a special category for the just-injected called “the extract.” However, those who die while in the extract are categorized as vaccinated (their death and small contribution of person-years would go into the 1st dose < 21 days buckets. It is therefore of no hazard that those not in the extract are considered “unvaccinated” — because the extract reflects and represents vaccination.

Clare Craig’s examination of apparent excluded deaths (deaths among those who do not meet PHDA inclusion requirements) does not seem to show any meaningful difference in death rates in the recorded vaccinated (and it should not, since inclusion in the PHDA is not based on vaccination).

ONS ghosts Part 1: Deaths among the ghost population

The only “big”-seeming difference is in the youngest age set; however, this group has very low rates of death, and so the y-axis is single digits. In the older groups, this difference is of a similar absolute scale, and thus acts like mere “noise” or fuzz on the plot.

It does not matter if exclusions are biased toward more likely death, because very few die-ers are excluded. The recorded rate loses a small amount of precision but is generally the same.

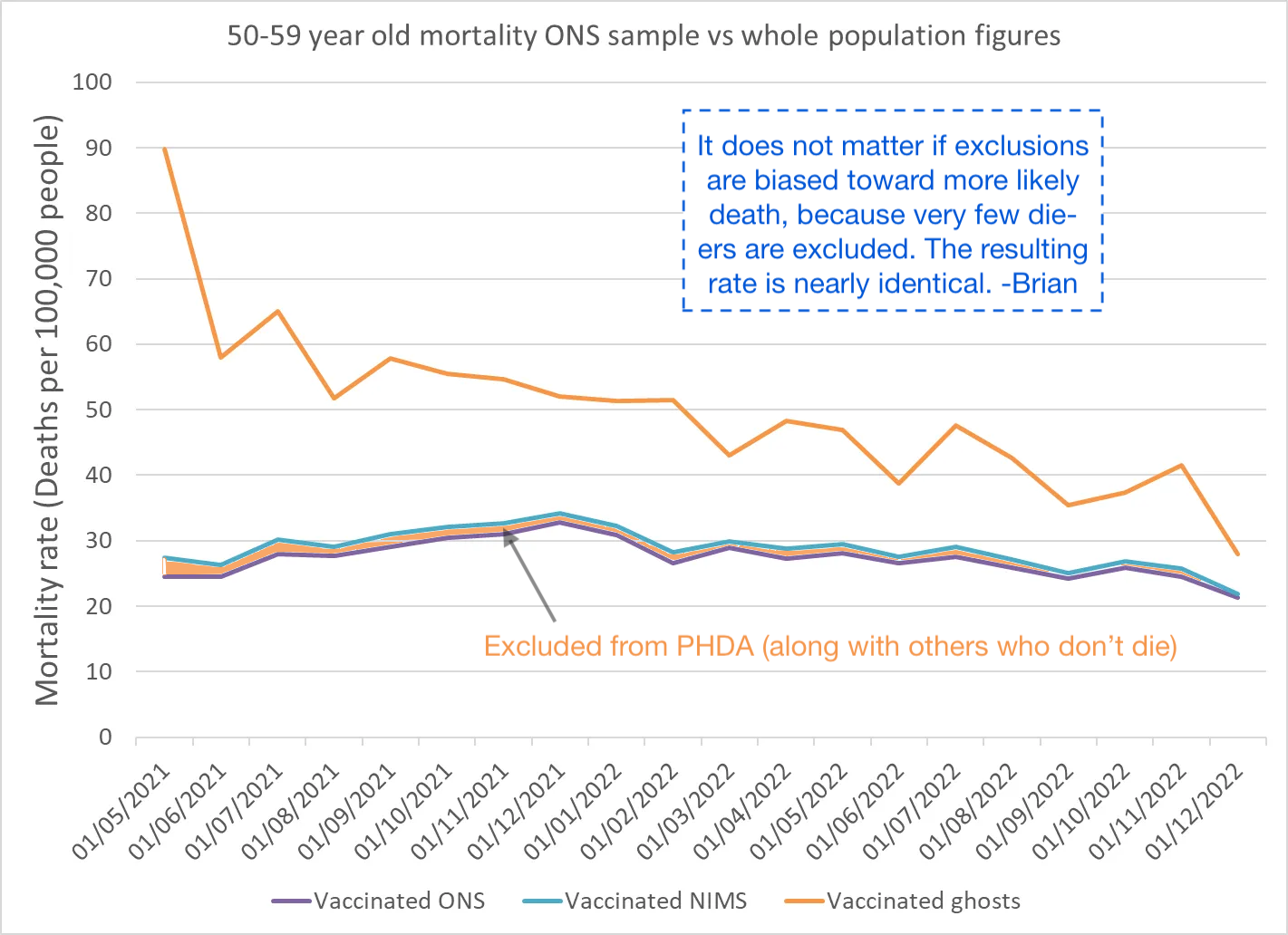
However, her calculations do find an apparent difference in death rates in the “unvaccinated.” This, however, merely recycles the same problem that the PHDA exclusions are designed to fix: It is unknowable whether everyone deemed “unvaccinated” in NIMS is actually still in contact with the system. The denominator is not accurate:

There is thus no way to divine to what extent the resulting difference in rates is demonstrating a deaths bias in the ONS-included unvaccinated cohort vs. demonstrating a broken denominator in NIMS (i.e., the rates used to measure “ghosts” is imaginary).

In the end (as in the beginning), it is the so-called “unvaccinated” in the NIMS invite list which has been excluded by the ONS who are full of “ghosts.”

2. See “The Panera Kingdom Problem.”

3. Stirrup, O. et al. “Effectiveness of successive booster vaccine doses against SARS-CoV-2 related mortality in residents of Long-Term Care Facilities in the VIVALDI study.” medrxiv.org

See also the language surrounding original vaccine recommendations:

https://www.bmj.com/content/372/bmj.n421

The schedule of priority groups, defining the order in which members of the public should receive the vaccine, was devised by the government’s Joint Committee on Vaccination and Immunisation, made up of scientists, doctors, and others. In line with WHO guidance, first up are care home residents and health workers, then older and clinically extremely vulnerable people. Among those excluded from the mass vaccination plan at present are pregnant women, children under 16, and those with health conditions that put them at very high risk of serious outcomes. All eligible UK adults are due to be offered a vaccine by the autumn.